문제
https://www.acmicpc.net/problem/9084
9084번: 동전
우리나라 화폐단위, 특히 동전에는 1원, 5원, 10원, 50원, 100원, 500원이 있다. 이 동전들로는 정수의 금액을 만들 수 있으며 그 방법도 여러 가지가 있을 수 있다. 예를 들어, 30원을 만들기 위해서는
www.acmicpc.net
왜 틀렸을까?
이 문제에 어떻게 DP를 적용할지 생각이 나지 않았다.
그리고 다른사람의 풀이도 보고 설명도 많이 들었지만 과정이 명확하게 이해가 되지 않았다.
나처럼 동전이 도저히 이해가 되지 않았던 사람을 위해 최대한 친절하게 풀어서 설명해보려고 한다.
문제 풀이 방식
많은 분들이 1차원 dp를 사용해서 풀었는데,
나는 1차원 dp table를 사용하는 방식으로는 이해가 잘 되지 않다가
마지막에 2차원 dp table의 설명을 듣고(GOD rohagru) 문제풀이 방식이 이해가 되었기 때문에 여기서도 2차원 dp table을 이용해서 설명을 진행한다.
먼저 문제가 원하는 바를 정확하게 이해해야 한다.
문제는 우리에게 주어진 금액을 만드는 모든 방법(가지수)의 개수를 물어보고 있다.
우리는 방법의 개수를 세야 하는데 여기서 사용하는 동전의 개수는 중요하지 않다!!
이 점을 주의하고 본격적인 문제풀이에 들어가 보자.
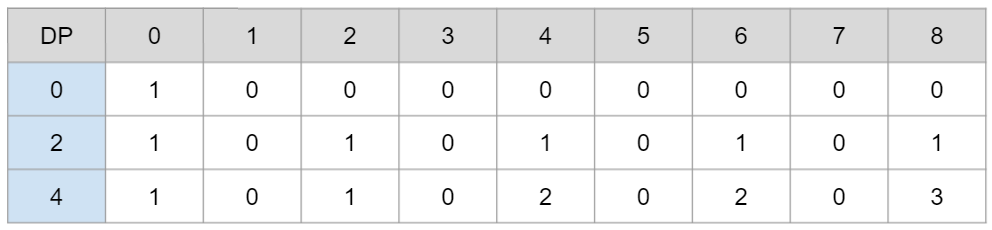
우리는 2원과 4원으로, 8원을 만들어 보려고 한다.
여기 2차원 dp table이 있다.
행은 우리가 가지고 있는 동전 (2원, 4원)
열은 우리가 만들어야 하는 금액을 의미한다.

일단 0원을 만들 수 있는 가지수를 1로 초기화시킨다.
이는 어떤 동전이든 0원을 만들 수 있는 '가지수'는 무조건 1가지 존재한다는 의미이다.
생각해 보면 2원짜리 동전 0개로 0원을 만들 수 있다.
4원짜리 동전 0개로도 0원을 만들 수 있다.
그러니까 어떤 동전이든 0원을 만들 수 있는 가지수는 무조건 1개가 존재한다.

지금은 4원을 생각하지 말고(검은색으로 가려버리고) 내 수중에는 2원만 있다고 생각하자.
만들고자 하는 금액인 2원(보라색으로 표시)을 만났을 때, 보라색 2원에서 내가 가진 2원을 냅다 빼버린다.
그 후에 2원을 뺀 나머지 금액으로 만들 수 있는 가지수를 살펴본다.
지금 상황에서는 나머지 금액이 0원이다. 즉 살펴보아야 할 DP칸은 DP[0]이다( DP[2-2] = DP[0] ). 앞에서 설명했듯이
2원으로 0원을 만들 수 있는 가지수는 무조건 1가지가 존재하기 때문에(DP[2-2]=DP[0]=1) 보라색 2를 만들 수 있는 가지수는 DP[0]의 값인 1이 된다. (DP[2] = DP[0] = 1)
상식적으로도 2원짜리 동전을 가지고 2원을 만드는 데는 1가지 방법이 존재한다.
이제 2원으로 3원을 만드는 가지수를 살펴볼까?

3원을 만났으니까 3원에서 2원을 냅다 빼면 1원이 되는데, 2원으로 1원을 만들 수 있는 가지수는 존재하지 않는다(DP[1]=0). 따라서 DP[1] = 0 을 가져와서 0이 된다.
다음으로 2원으로 4원을 만드는 가지수를 살펴보자.

이제 어떤 작업을 수행할지 대충 감이 오지 않는가?
1. 일단 만들고자 하는 값에서 냅다 2(현재 동전의 값)를 뺀다.
- 지금 여기서는 DP[4-2]를 의미
2. '나머지 값'을 만들 수 있는 가지수를 DP table에서 살펴보고 그 값을 그대로 가져온다.
- DP[4-2] = DP[2] = 1 이므로 1을 그대로 가져온다.
- DP[4] = 1
일반적인 경우로 확장해서 생각해보자.
2원으로 X원을 만들 수 있는 가지수가 몇 가지인지를 알고 싶다면,
2원으로 (X-2)원을 만들 수 있는 가지수가 몇 가지인지 살펴보면 된다.
2원으로 X-2원을 만들 수 있는 가지수는, (X-2)+2원의 가지수와 같다.
헷갈림 방지!!
2원으로 만들 수 있는 가지수를 세고 있기 때문에 2원짜리 동전의 개수가 추가되는 것은 가지수가 늘어나는 것이 아니다!!
이 방식으로 2원으로 만들 수 있는 값의 가지수를 쭉쭉 채워갈 수 있다.

2원으로만 만들 수 있는 값들의 가지수를 다 채웠으니까
이제 4원으로 만들 수 있는 값들의 가지수도 살펴보자.
그런데 여기서 잠깐!
6원같은 경우는 4원만 가지고는 만들 수 없지만, 2원짜리 1개와 4원짜리 1개로 만들 수 있다.
즉, 4원칸에서는 2원으로만 만들 수 있는 가지수를 4원 칸에 가지고 온 다음에 시작해야 한다.

이렇게 해주면, 지금은 4원만 사용하는 것이 아니라 우리에게 4원과 2원 둘다 사용하는 셈이 된다.
나는 이제 동전 4를 가지고 있다. 동전 4는 4의 값부터 만들 수 있기 때문에 4부터 보겠다.

2원 때와 마찬가지로
만들고 싶은 값 4(보라색)에서 내가 지금 가진 동전 4를 냅다 뺀다.
그럼 DP[4-4] = DP[0]을 보고 값이 1이기 때문에 1을 가져온다(주황색). (동전 4원으로 4를 만들 수 있는 개수는 1가지)
그런데 이미 2로 만들 수 있는 4의 가지수를 업데이트 해줬기 때문에(파란색) 1+1 = 2의 가지수를 가지게 된다.
이런 식으로 2원과 4원을 모두 사용한 가지수를 DP table에 저장해줄 수 있다.
5원은 만들 수 없으므로 넘어가고,

6원일 때를 살펴보면 DP[6-4] = DP[2] = 1인데, 2원만으로 6원을 만들 수 있는 개수 1가지가 있으므로
현재 DP[6]은 4원으로 만들 수 있는 가지수(주황), 2원으로 만들 수 있는 가지수(파랑)의 값들을 모두 합친 형태로 저장되게 된다.
7원은 만들 수 없으므로 넘어가고,
마지막 8원을 만드는 경우의 가지수를 살펴보자!

8원에서 4원을 빼고, 4원과 2원으로 만들 수 있었던 DP[4] = 2의 값(주황색)과 2원만으로 만들 수 있던값(파란색)을 모두 더해서 3가지의 경우의 수가 답으로 출력되게 된다.
실제로도 2원과 4원으로 8을 만드는 경우는
2+2+2+2
2+2+4
4+4
로 총 3가지가 있음을 알 수 있다.
코드
행에 0번째 줄을 추가하여 코드를 구현했다.(2일때도 똑같은 로직을 실행하기 위해)
2차원 DP table 코드
내가 설명한 로직을 그대로 코드로 옮기면 이렇게 된다.
import sys
T = int(sys.stdin.readline())
for _ in range(T):
N = int(sys.stdin.readline())
coins = list(map(int, sys.stdin.readline().split()))
coins.insert(0, 0)
M = int(sys.stdin.readline())
dp = [[0] * (M+1) for i in range(N+1)]
for i in range(N+1):
dp[i][0] = 1
for j in range(1, N+1):
for i in range(1, M+1):
dp[j][i] = dp[j-1][i]
if i-coins[j] >= 0:
dp[j][i] += dp[j][i-coins[j]]
print(dp[N][M])1차원 DP table 코드
지금까지의 설명을 이해하고 나면 2차원 배열을 1차원에서 실행시키는 거구나! 라고 이해하게 된다.
import sys
T = int(sys.stdin.readline())
for _ in range(T):
N = int(sys.stdin.readline())
coins = list(map(int, sys.stdin.readline().split()))
M = int(sys.stdin.readline())
dp = [0] * (M+1)
dp[0] = 1
for coin in coins:
for i in range(1, M+1):
if i >= coin:
dp[i] += dp[i-coin]
print(dp[M])'sw사관학교정글' 카테고리의 다른 글
| [week05] 포인터 이해하기 - part.1 (0) | 2021.12.09 |
|---|---|
| [week05] 코드리뷰 - 류석영 교수님 (0) | 2021.12.09 |
| [week03] 백준 11725번 python 풀이 (0) | 2021.11.29 |
| [week03] 백준 18405번 python 풀이 (0) | 2021.11.28 |
| [week02] 백준 5904번 파이썬 풀이 (2) | 2021.11.18 |